35. Search Insert Position

题目描述：

給定一個排序陣列和一個目標值，請在陣列中找到目標值，並返回其索引。如果目標值不在陣列中，則返回它將會按順序插入的位置。

你必須編寫一個時間複雜度為 O(log n) 的算法。

Example 1:

• Input: nums = [1,3,5,6], target = 5
• Output: 2

Example 2:

• Input: nums = [1,3,5,6], target = 2
• Output: 1

解題思路
在 LeetCode 題目中，經常會遇到需要在排序陣列中尋找目標值的問題。這類型題目通常會使用 Binary Search（二分搜索法） 來尋找目標值。

二分搜索法的基本思路是：在已排序的陣列中，先找到中間值，然後將陣列分為兩部分。如果目標值小於中間值，則在左半部分繼續進行二分搜索；如果目標值大於中間值，則在右半部分繼續進行搜索。由於每次搜索都將陣列的數量減少一半，因此時間複雜度為 O(log n)，這正好符合本題的要求。

值得一提的是，在執行二分搜索法時，使用頭尾雙指針 left 和 right 來表示搜索範圍。結束條件有兩種可能：

1. left <= right：適用於標準的二分查找，當需要遍歷整個搜索區間並確保所有元素都被檢查到時使用。
2. left < right：適用於找到某個條件下的插入位置或其他邊界問題時使用。

讀者千萬不要一概而論地使用 left <= right，因為這樣很容易導致錯誤的結果。那麼，如何判斷應該使用哪種結束條件呢？答案很簡單——像這道題一樣，畫出二分搜索法的過程，特別是最後關鍵的一步，來確定應該採用哪個結束條件。通過仔細分析和演算，可以避免因錯誤選擇結束條件而導致的計算偏差。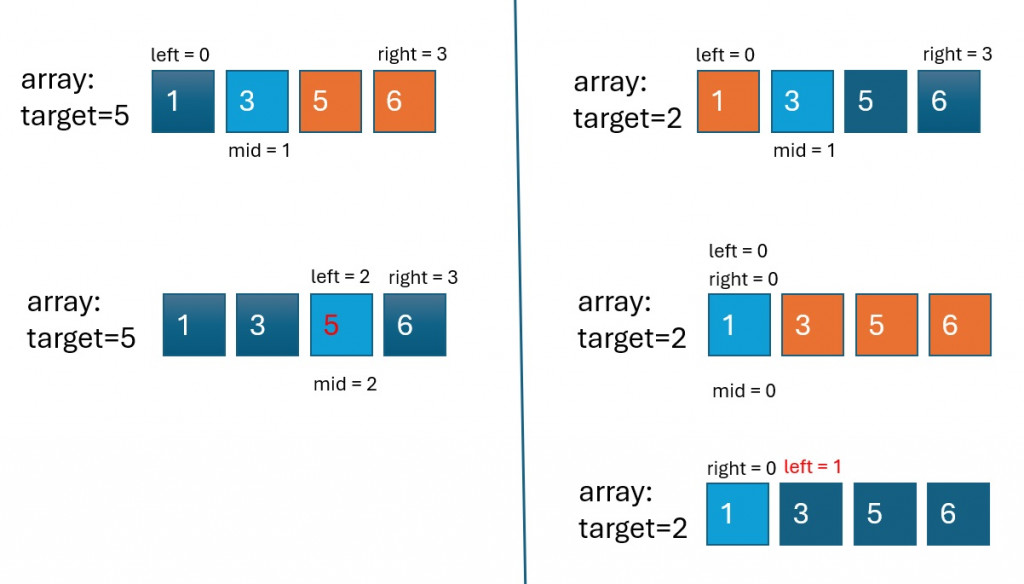

var searchInsert = function(nums, target) {
    let left = 0;
    let right = nums.length - 1;

    while (left <= right) {
        let mid = Math.floor((left + right) / 2);
        if (nums[mid] === target) {
            return mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }

    return left;
};

時間複雜度：O(log n)，因為我們使用了二分搜索算法。
空間複雜度：O(1)，只使用了常數空間來存儲指針。

總結:
這道題目可以歸類為「Binary Search」。很明顯，這題的設計目的是讓讀者學習如何使用二分搜索法來尋找目標值。之後的 LeetCode 題目中，二分搜索法仍會經常出現，只是題目可能會有所變形而不易察覺。不過，當題目中出現「排序陣列」和「搜尋唯一解」這兩個關鍵詞時，使用二分搜索法的可能性就會很高，不妨先嘗試這個方法來解題，往往問題一下就解決了。